Résumé :
Les modèles à effets mixtes sont très utiles pour modéliser différentes sources de variabilités au sein d’une population, via des effets fixes et des effets individuels. L’un des enjeux principaux en modélisation est de bien discriminer les deux types d’effets. Du point de vue statistique, il s’agit de tester la nullité des composantes de la variance du modèle, ce qui est un problème méthodologique complexe. Les propriétés du test classique du rapport de vraisemblance qui permet de répondre à cet enjeu ont été établies récemment dans ce contexte. Cependant, le calcul précis de la statistique de test reste un défi. Des chercheurs de INRAE et de l’Université de Lille ont développé une méthode pour calculer effacement ce ratio et ont établi ses garanties théoriques. Du point de vue pratique, être capable d’identifier les effets individuels est crucial : par exemple dans le contexte de la modélisation des interactions génotypes environnements via des modèles mécanistes, identifier les effets individuels revient à identifier les paramètres du modèle qui varient avec les génotypes, permettant ainsi de cibler des leviers d’action privilégiés pour sélectionner des variétés adaptées à différents environnements.
Contexte et enjeux :
Les modèles à effets mixtes sont très utiles pour modéliser différentes sources de variabilités au sein d’une population, via des effets fixes et des effets individuels. L’un des enjeux principaux en modélisation est de bien discriminer les deux types d’effets. Du point de vue statistique, il s’agit de tester la nullité des composantes de la variance du modèle. Ce problème est complexe dans le cadre général parce que les paramètres de variance testés sont sur le bord de l’espace des paramètres. Récemment les garanties asymptotiques de la statistique du test de rapport de vraisemblance dans ce contexte non standard ont été établies. Cependant la statistique de test est difficile à calculer numériquement car elle s’exprime sous la forme d’un ratio d’intégrales. Du point de vue pratique, être capable d’identifier les effets individuels est crucial : par exemple dans le contexte de la modélisation des interactions génotypes environnements via des modèles de culture ou écophysiologiques, identifier les effets individuels revient à identifier les paramètres mécanistes du modèle qui varient avec les génotypes, permettant ainsi de cibler des leviers d’action privilégiés pour sélectionner des variétés adaptées à différents environnements.
Résultats :
Des chercheurs de INRAE et de l’Université de Lille ont développé une nouvelle méthode pour calculer efficacement un ratio d’intégrales, en particulier un ratio de constantes de normalisation. L’algorithme proposé est basé sur un schéma d’approximation stochastique qui combine judicieusement les avantages de méthodes existantes telles que le ratio importance sampling et le bridge sampling. Les auteurs ont étudié les propriétés théoriques de cet algorithme comme la convergence et la normalité asymptotique. Ils ont ensuite comparé sa précision à celle des méthodes existantes via la matrice de variance-covariance asymptotique. Ils ont en particulier mis en évidence que l’algorithme proposé est meilleur pour ce critère que les méthodes existantes. La méthode proposée est par ailleurs peu sensible à des contextes où les supports des deux intégrales sont quasi disjoints. Ce travail a été réalisé et financé au sein du projet ANR interdisciplinaire STAT4PLANT https://stat4plant.mathnum.inrae.fr.
Perspectives :
La méthode proposée permet le calcul efficace de ratios d’intégrales très généraux. Elle pourrait en particulier être facilement optimisée pour le calcul d’une unique constante de normalisation. De plus, dans le cas du test de rapport de vraisemblance pour des modèles emboités à variables latentes, il est possible d’optimiser l’algorithme en calculant simulanément les estimateurs du maximum de vraisembmance sous les hypothèses nulle et alternative et le ratio de la statistique de test. Ceci ouvrirait en particulier la possibilité de considérer des modèles statistiques à effets mixtes emboités combinés à des modèles mécanistes comme les modèles de culture en amélioration des plantes.
Référence correspondant au FM (du ou des articles, de l’ouvrage, du brevet… (avec DOI, ISSBN, N° brevet) Guédon, T., Baey, C. & Kuhn, E. Estimation of ratios of normalizing constants using stochastic approximation: the SARIS algorithm. Stat Comput 35, 166 (2025) doi.org/10.1007/s11222-025-10664-0
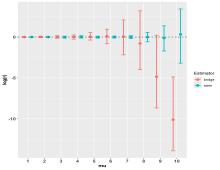
Illustration de l’influence de la taille de l’intersection des supports des deux intégrales du ratio sur l’efficacité des algorithmes SARIS et bridge sampling pour calculer le ratio d’intégrales. (T. Guédon, C. Baey, E. Kuhn).
