Résumé
Les modèles à effets mixtes sont très utiles pour modéliser différentes sources de variabilités au sein d’une population, via des effets fixes et des effets individuels. L’un des enjeux principaux en modélisation est de bien discriminer les deux types d’effets. Du point de vue statistique, il s’agit de tester la nullité des composantes de la variance du modèle, ce qui est un problème complexe. Des chercheurs de INRAE, de CentraleSupelec et de l’Université de Lille ont établi un résultat théorique asymptotique pour tester la nullité d’un sous-ensemble quelconque des composantes de la variance dans des modèles à effets mixtes très généraux et ont développé un package pour faciliter son application pratique, en particulier en agronomie, en génétique et en écophysiologie. Du point de vue pratique, être capable d’identifier les effets individuels est crucial : par exemple dans le contexte de la modélisation des interactions génotypes environnements via des modèles de culture ou écophysiologiques, identifier les effets individuels revient à identifier les paramètres mécanistes du modèle qui varient avec les génotypes, permettant ainsi de cibler des leviers d’action privilégiés pour sélectionner des variétés adaptées à différents environnements.
Contexte et enjeux : Les modèles à effets mixtes sont très utiles pour modéliser différentes sources de variabilités au sein d’une population, via des effets fixes et des effets individuels. L’un des enjeux principaux en modélisation est de bien discriminer les deux types d’effets. Du point de vue statistique, il s’agit de tester la nullité des composantes de la variance du modèle. Ce problème est complexe dans le cadre général parce que les paramètres de variance testés sont sur le bord de l’espace des paramètres. Du point de vue pratique, être capable d’identifier les effets individuels est crucial : par exemple dans le contexte de la modélisation des interactions génotypes environnements via des modèles de culture ou écophysiologiques, identifier les effets individuels revient à identifier les paramètres mécanistes du modèle qui varient avec les génotypes, permettant ainsi de cibler des leviers d’action privilégiés pour sélectionner des variétés adaptées à différents environnements.
Résultats : Des chercheurs de INRAE, de CentraleSupelec et de l’Université de Lille ont établi un résultat théorique asymptotique pour tester la nullité d’un sous-ensemble quelconque des composantes de la variance dans des modèles à effets mixtes très généraux. Ils ont considéré la statistique du test de rapport de vraisemblance et ont montré que sa loi asymptotique est une loi du chi-bar squared bien identifiée. Pour que ce résultat soit exploitable facilement par une large communauté d’utilisateurs de modèles à effets mixtes, en particulier en agronomie, en génétique et en écophysiologie, un package R varTestnlme a été développé et mis à disposition librement.
Perspectives : Dans de nombreux cas pratiques, les échantillons observés disponibles sont de petites tailles, ce qui peut remettre en cause la validité du résultat asymptotique présenté ci-dessus. Une méthode adaptée au cas d’un petit nombre de données est en cours de construction et d’analyse au sein du projet ANR interdisciplinaire STAT4PLANT https://stat4plant.mathnum.inrae.fr.
Valorisation :
C. Baey, E. Kuhn. varTestnlme: Variance Components Testing for Linear and Nonlin-
ear Mixed Effects Models. R package version 1.3.5, URL https://CRAN.R-project.org/
package=varTestnlme, 2023.
Références bibliographiques :
C. Baey, E. Kuhn. varTestnlme: an R package for Variance Components Testing in Linear and Nonlinear Mixed-effects Models. Journal of statiscal software, Vol. 107, Issue 6, 2023.
C. Baey, P.H. Cournède, E. Kuhn. Asymptotic distribution of likelihood ratio test statistics for variance components in nonlinear mixed effects models. Computational Statistics and Data Analysis, Vol. 135, pp 107--122, 2019.
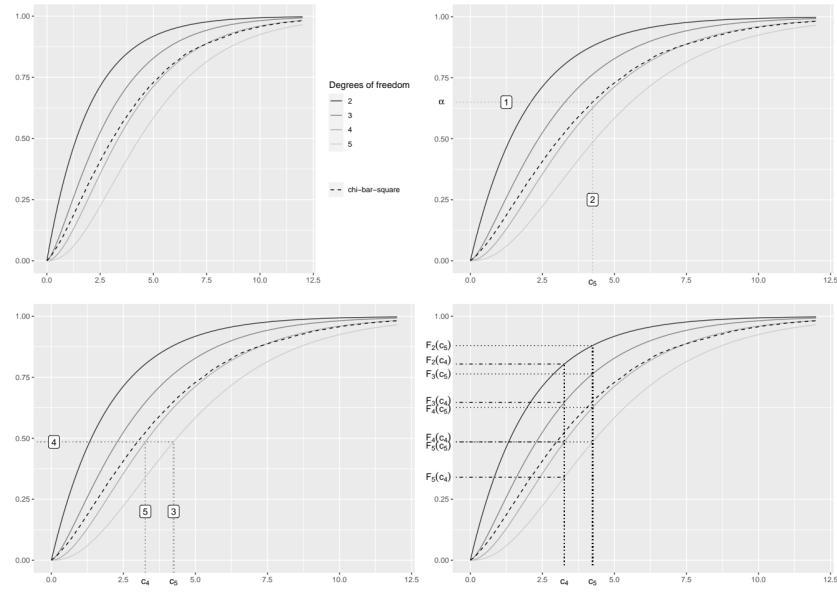
Illustration du choix de la suite croissante cd1+2 < · · · < cd2 utilisée dans l’algorithme pour approximer la loi du chi-bar squared (C. Baey, E. Kuhn).