Le modèle de Gibbs de tessellation permet de représenter une large gamme de données spatiales. Il peut être utilisé pour modéliser des paysages agricoles. Nous proposons une démarche statistique qui permet de générer des tessellations dotées de caractéristiques des paysages réels. Les paramètres du modèle sont estimés par la méthode du maximum de vraisemblance Monte Carlo. Les simulations nécessaires pour calculer l’estimateur sont réalisées à l'aide d'une dynamique de Metropolis-Hastings-Green adaptée. Afin de réduire le coût computationnel, un estimateur de la pseudo-vraisemblance est proposé pour l'initialisation de l'optimisation de la vraisemblance. L'évaluation du modèle est basée sur des tests d'enveloppes globales, appliqués à l'ensemble des statistiques fonctionnelles de la tessellation.
Contexte et enjeux : L'approche stochastique pour modéliser des paysages agricoles permet de prendre en compte l'hétérogénéité spatiale des paysages, tout en conservant les principales caractéristiques qui différencient des patrons paysagers. 'Cette propriété présente un intérêt pratique dans l’étude des interactions entre le paysage et les processus agroécologiques étudiés à cette échelle. Alors que le rôle de la composition du paysage sur les processus fait objet de plusieurs études, l'impact de la géométrie de ses éléments s’avère plus délicat à mettre en évidence, ceci en raison de manque d'outils adaptés. C’est dans ce contexte qu’un modèle stochastique des parcellaires agricoles est proposé en 2013 dans l’Unité MaIAGE. Un parcellaire y est représenté par une partition polygonale de l'espace, appelée une tessellation en T. Chaque sommet d'une tessellation en T possède trois côtés adjacents, dont deux qui sont alignés. C'est une propriété partagée avec des parcellaires agricoles : la majorité de sommets des parcelles sont de même type. Le modèle de Gibbs est défini par la loi de probabilité sur l'espace des tessellations en T. Cette loi met en jeu des caractéristiques des parcelles qu’on cherche à contrôler. En calibrant les paramètres du modèle, l’utilisateur peut générer des tessellations qui respectent des contraintes géométriques basées sur des caractéristiques données en entrée du modèle. On peut ainsi faire varier les formes et les tailles des parcelles. Le simulateur du modèle est mis en place et on s’interroge sur la possibilité de paramétrer le modèle pour simuler des tessellations qui ressemblent à des parcellaires agricoles. Le travail sur le modèle se concentre sur des méthodes statistiques utilisées pour atteindre cet objectif.
Résultats : Nous proposons une approche statistique intégrée pour le modèle de Gibbs. Pour estimer les paramètres, nous préconisons d’abord l’estimateur de maximum de pseudo-vraisemblance, construit et étudié spécifiquement pour ce modèle. Le principal avantage de cette méthode est son faible coût computationnel. En revanche, l'estimateur devient biaisé lorsque le domaine de tessellation est petit. Par conséquent, nous recommandons dans un deuxième temps l'utilisation de la vraisemblance Monte Carlo pour affiner l’estimation initiale. Nous proposons également la procédure de tests basés sur les descripteurs de tessellation pour évaluer la qualité du modèle. Les résultats indiquent dans quelle mesure le modèle s'ajuste aux données et fournissent des lignes directrices pour améliorer le modèle
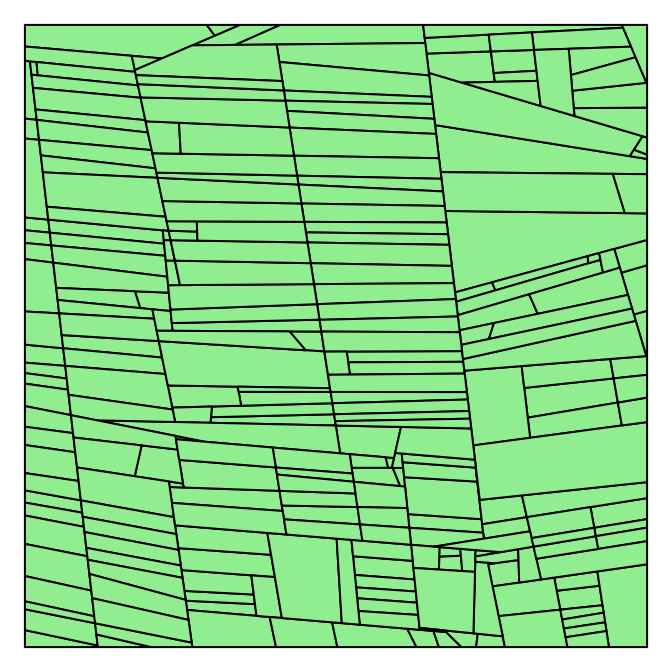
Cette démarche a été mise en place pour comparer trois paysages agricoles français, approximés préalablement par des tessellations en T (Figure 1). Un modèle de Gibbs proposé pour ces paysages contrôle quatre caractéristiques: l'échelle des paysages, la variabilité des aires des parcelles, leurs élongation et les angles entre les côtés des parcelles. La vérification du modèle est basée sur des simulations : la Figure 2 présente les distributions de quatre caractéristiques calculées pour des tessellations simulées selon le modèle ajusté. On constate que toutes les distributions sont centrées sur des valeurs observées dans les paysages d'origine. Le modèle permet alors de simuler des tessellations dotées de caractéristiques de paysages réels.
Perspectives L'utilisation du modèle de Gibbs a pour objectif de caractériser statistiquement et morphologiquement les paysages agricoles. Le cadre de modélisation, illustré ici sur l'exemple des paysages, peut être étendu à d'autres données spatiales qui peuvent être approximées par des tessellations en T. L'objectif est de fournir aux praticiens un outil de modélisation centré sur les propriétés géométriques de telles données, pertinentes pour des applications.
Valorisation :
L’article « Statistical inference for random T-tessellations models. Application to agricultural landscape modeling » a été accepté dans Annals of theI Institute of Statistical Mathematics en novembre 2023.
Références bibliographiques :
1) K. Kiêu, K. Adamczyk-Chauvat, H. Monod, R.S. Stoica (2013). A completely random T-tessellation model and Gibbsian extensions. Spatial Statistics, 6:118-138.
2) K. Kiêu, K. Adamczyk-Chauvat (2015). Pseudolikelihood inference for Gibbsian T-tessellations. . . and point processes. https://hal.archives-ouvertes.fr/hal-02793013.
3) K. Adamczyk-Chauvat, K. Kiêu (2015). LiTe. http://kien-kieu.github.io/lite.